馬場 吉弘（同志社大学）

1. 概要

FDTD（Finite Difference Time Domain）法⁽¹⁾は，Maxwell方程式の磁界Hおよび電界Eに関する2 つの回転の式（アンペアの法則∇×H =σE+ε ∂E/∂tとファラデーの法則∇×E = −μ ∂ H/∂ t。ただし，σ は導電率，ε は誘電率，μ は透磁率）を差分化して求めた電界および磁界の更新式を用いて，解析空間の電磁界の挙動を時間領域で計算する手法である。この手法を用いた解析は直交座標系で行なわれるのが一般的で，解析対象の導体系を含む全ての解析空間を微小直方体または立方体（セル）に分割する必要がある。セルの各辺要素には電界が割り当てられ，セルの各面の中心にはそれに垂直な磁界が割り当てられる。これは，図1に示すように，互いに1/2 セルずつずれた電界の3 次元格子と磁界の3 次元格子が存在するものと考えてもよい。これにより，電界要素の周囲には必ず（長方形または正方形の）磁界ループが存在し，磁界要素の周囲には必ず電界ループが存在することになり，上述のMaxwell 方程式を計算するのに適した構成となる。原理的には，格子分割した各セルに対して媒質定数を設定可能なため，複雑な境界を有する導体系や，モーメント法では取扱いが困難な体積を有する導体や板状の導体も容易に取り扱うことができる。

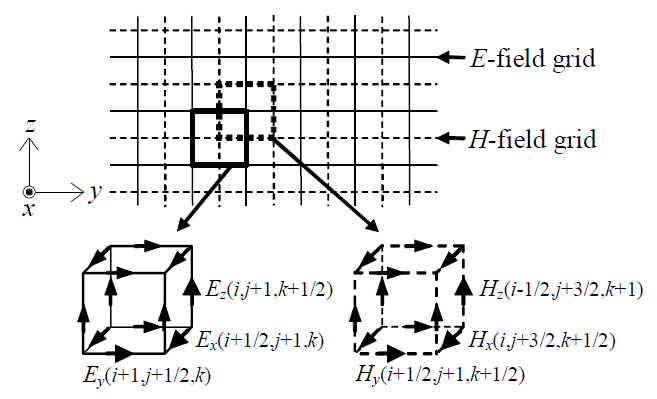
図1　FDTD計算における電界，磁界セルの配置

2. 磁界，電界の計算式

セルのx，y，z 各方向の辺長をΔx，Δy，Δz，計算時間ステップ幅をΔt とすると，座標（iΔx, (j+1/2)Δy, (k+1/2)Δz），時間 (n+1/2)Δtにおけるx方向の磁界H_x^n+1/2 (i, j+1/2, k+1/2)は，ファラデーの法則

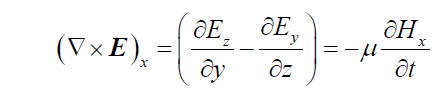
の電界の空間微分および磁界の時間微分を次のように差分近似することで導かれる。

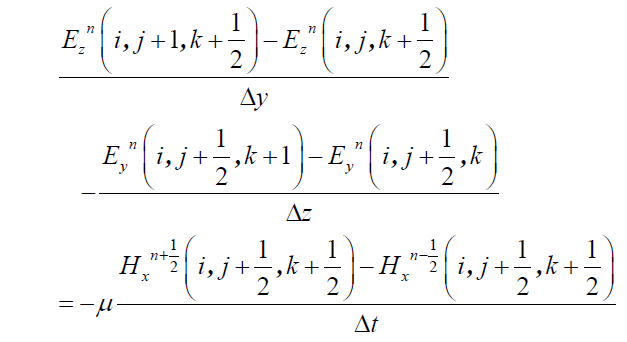
より，

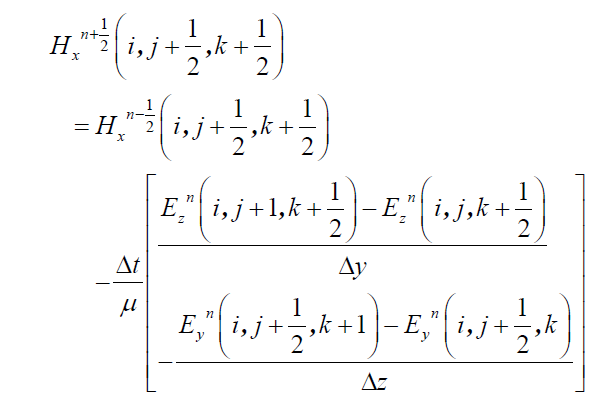
が得られる。この式は，解析空間中の任意の点の任意の時間における磁界の値は，その点のΔt 時間前の磁界の値と，その磁界を囲む4 つの電界のΔt/2 時間前の値から求められることを示している。上記と同様にして，y，z 方向の磁界H_y，H_z の更新式も求められる。また，アンペアの法則の時間微分および空間微分を同様に差分化することで，x，y，z各方向の電界E_x，E_y，E_z の更新式も求められる。これらの磁界および電界の更新式を，時間的に交互に計算することで，解析空間内の電磁界の挙動を求めることができる。

3. 電力・エネルギー分野への応用例

電力・エネルギー分野においては，これまでに接地電極，電力ケーブル，架空配電線，送電鉄塔，風力発電設備等のサージ解析やガス絶縁管路内の部分放電電磁界パルスの伝搬特性解析に本手法が適用されている(2)。さらに，FDTD 法による電磁界・サージ解析のための接地電極の土中放電モデル，アークホーン間のフラッシオーバモデル，避雷器モデル等も提案されるに至っている。

文献

(1) K. S. Yee：”Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media”, IEEE Trans. on Antenas Propagat.., Vol. 14, No. 3, pp.302-307 (1966)

(2)過渡数値電磁界解析手法の応用調査専門委員会：「FDTD法を中心とした数値電磁界解析手法によるサージ解析の最新動向」，電気学会技報，No. 1216 (2011)

【電気学会論文誌B，131巻6号，2011に掲載】