用語解説 第44回テーマ: 粒子群最適化(PSO) ~生物の採餌行動を模擬した最適化手法~
2020/08/27

澤 敏之 〔(株)日立製作所〕
1. はじめに
PSO(Particle Swarm Optimization)(1)は1995 年にJ. Kennedy とR. Eberhart により開発された最適化手法である。基本的な考え方は,鳥の群れが餌を見つける行動をもとに導かれた「情報を群れ全体で共有する」ことにある。群れを構成する個体が自由に行動するのではなく,群れを構成する個体固有の情報と群れ全体共通の情報を融合させて,一定の規則に従って行動する。
2. PSO のアルゴリズム
PSO において群れを構成する各個体は,現在の“位置(状態量)”とそのときの“速度”の情報を持っている。この位置と速度の情報から次世代の各個体の位置を更新する。
目的関数 f (x) は変数である状態量 x によって一意に決定されるものとする。各個体はそれぞれの個体の最良位置pbest (personal best)と群れ全体の最良位置gbest (global best)に近づく方向に(1)式で速度を修正しながら現在位置(探索点)を(2)式により更新する。PSO における探索点の修正方法を図1 に示す。
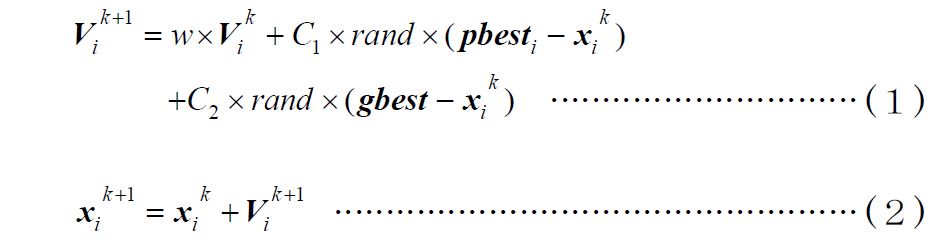
ただし,i は個体番号, xiは各個体の位置, Vi は各個体の速さ,rand は0~1 の一様乱数,k は探索更新回数(世代数), C1, C2,wは定数を示す。 C1, C2は加速係数,w は速度に関する慣性係数である。
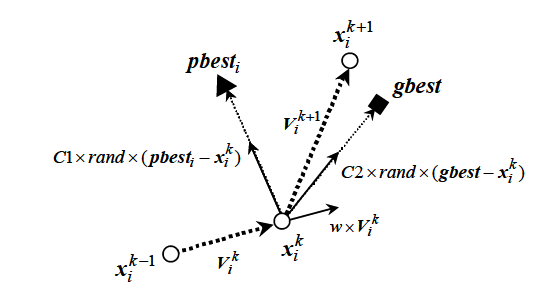
図1 PSOの探索点の決定方法
(1)式により各個体のこれまでの最良値および集団の最良値に確率的に近づくような速度が求められる。
PSO のアルゴリズムを示す。
〔Step 1〕 個体の位置xiと速度 Vi を乱数で初期化
〔Step 2〕 最小化したい目的関数値 f (xi) を評価
〔Step 3〕 個体のそれまでの最良値 f ( pbesti)と比較。もし「 f (xi ) < f ( pbesti )」ならば「 f ( pbesti ) = f (xi )」,「pbesti= xi」と更新
〔Step 4〕 群れ全体の最良値 f (gbest) と比較。もし「 f (xi) < f (gbest) 」ならば,「 gbest = xi」と更新
〔Step 5〕 (1)式で速度を更新し,(2)式で位置を更新
〔Step 6〕 Step 2 に戻り,収束条件を満たすまで繰り返す
3. どんな問題に適用できるの?
線形計画法,非線形計画法で厳密な最適解が求められる問題より,目的関数,制約条件が複雑な問題や計算時間のかかる大規模問題への適用に適しており,目的関数,制約条件を数式で定義できれば適用できる。目的関数を最小化する問題へ適用するときは,一般的に,採用する評価関数g(x)は(3)式のように,制約条件違反が生じたときには正の値になり,違反がないときゼロとなるペナルティ関数 p(x)を加算する。
![]()
α :十分大きな正の値
評価関数を小さくする解を求めようとするため,制約条件違反がある解より違反がない解を,制約条件違反がない解の中では目的関数が小さい解を探索することになる。もちろん,制約条件を満たさない解や最適解からほど遠い解しか求められないこともあり,残念ながら万能薬ではない。
(1), (2)式から分かるように,PSO は実数変数を対象としている。問題の特徴を捉えて定式化することにより,比較的簡単なアルゴリズムであるにもかかわらず,比較的高速に良い解を求めることができる(2)。
4. おわりに
PSO は電圧無効電力などの実数変数問題だけではなく,同様の考え方を適用して発電所起動停止計画などの組合せ最適化問題など広く電力系統の最適化問題へ適用(3)されている。
初期解,定式化方法,パラメータ設定の方法など,対象とする電力系統の問題の知識が深いほど,より高速に,より良い解を求めることが期待できる。
文献
(1) J. Kennedy and R. Eberhart : “Particle swarm optimization”, Proc. of IEEE Int. Conf. Neural Networks, Vol.4, pp.1942-1948 (1995-10)
(2) 「電力系統へのメタヒューリスティクス応用技術」,電気学会技術報告,Vol.923 (2003-6)
(3) 相吉英太郎・安田恵一郎:メタヒューリスティクスと応用,電気学会(2007-7)

