用語解説　第88回テーマ：　パレート最適解

村田 晃伸 （国立研究開発法人産業技術総合研究所）

1. はじめに

2 つ以上の目的関数を持つ最適化問題（多目的最適化問題）では，すべての目的関数を同時に最小（最大）化する解は，多くの場合に存在しない。そのような多目的最適化問題においても解の最適性を定義することは有意義であり，そのひとつがパレート最適解である。パレート最適性の概念は，経済学者であるパレート（Vilfred Pareto 1848～1923）が社会における財・サービスの配分の優劣を判断するための基準として提唱したのが始まりである⁽¹⁾。

2. パレート最適解の概念

2 つの目的関数U1，U2 を持つ多目的最小化問題の目的関数値が，U1-U2 平面に分布する様子を図1 に例示する。右下がりで下に凸な曲線PQ の右上に描かれた点A を含む灰色の領域が，実行可能な解の目的関数値が取り得る範囲を表す。具体例としては，汚染対策における汚染物質の排出量(U1) と対策コスト(U2) の関係が図1 のようになる。灰色の領域内部の点A が表す解に対しては，曲線PQ 上の点B が表す解のようにすべての目的関数値が点A の解よりも小さい解が存在する。一方，曲線PQ 上の点B が表す解の場合は，どれか1 つの目的関数値がより小さい別の解を選ぶと，少なくとも1 つの他の目的関数値は大きくなってしまう。この条件を満たす解をパレート最適解という。この例では，曲線PQ 上の解はすべてパレート最適解の条件を満たす。通常，パレート最適解は多数個存在する。

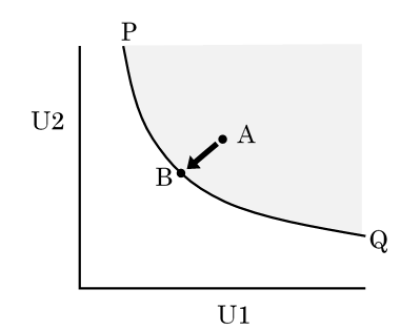
図1　2つの効用の無差別曲線

文 献

(1) 西村和雄：現代経済学入門 ミクロ経済学，岩波書店 (1996)

【電気学会論文誌B，138巻，7号，2018に掲載】