用語解説　第95回テーマ：　高温超電導電流リード

篠原 靖志 〔（一財）電力中央研究所〕

1. はじめに

サポートベクタマシン (Support Vector Machine)⁽¹⁾は，学習データから高精度の判定基準を学習できる代表的機械学習手法である。信頼性の高い電力設備を対象とした診断基準などの学習では，利用可能な正常データは多いが異常データは少ない。従って少数の異常データでも高精度の判定を行える手法が重要となる。SVM は，この点で古典的判定手法やデータ数が要る深層学習などにない特徴を持つ。

2. 線形SVM の原理と非線形SVM への拡張

線形SVM は，入力X（属性数m）の正常・異常を各属性の線形判別式の正負で判定する。この時，判別面に最も近い学習データ（サポートベクタ；支持点）との距離（マージン；余裕分）が小さい（図1 細い点線）と，測定等による入力の変化（誤差混入）で誤判定が生じ易い。SVM ではマージンが最大の判別面（図1 太い実線）を用い，誤判定が生じにくくしている。線形SVM の判別面は，判別面周辺の少数のサポートベクタX_i のみで定まり，判別式は，サポートベクタX_i と入力X の内積<X_i, X> の線形和で表される（なお，内積<Z, X> とはZ, X の各要素の積の和のことである）。従って，正常・異常の境界付近のデータを一定量集められれば，総データ数は少なくても高精度の判定基準が学習できる。

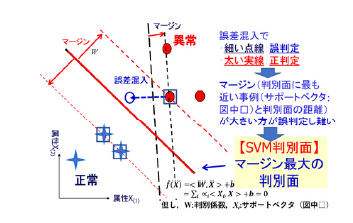
図1　線形SVMの原理

非線形SVM では，入力X の代わりに高次元特徴量φ (X)，内積<Z, X> の代わりにカーネル関数と呼ばれるK(Z, X) =<φ (Z), φ (X)> を用いて非線形判別を行う（図2）。データ間の類似度を示すRBF カーネルexp(−g||X−Z||²) はしばしば利用される代表的カーネル関数で，代表事例（サポートベクタ）との類似度に基づく判定基準が得られる。SVM に対しては，多クラス判定や多出力判定を行う多クラスSVM，構造化SVM など各種拡張が行われている。

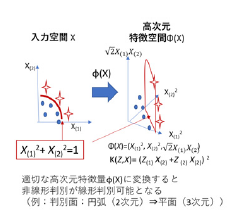
図2　非線形SVM

文献

(1) C. Cortes and V. Vapnik : “Support vector networks”, Machine Learning, Vol.20, pp.273-297 (1995)

【電気学会論文誌B，139巻，2号，2019に掲載】