用語解説 第112 回テーマ： 粒子法（Particle Method）
tweet
facebook
LINE
ブックマーク
コピー
印刷2020/10/09
宮坂 史和 （大阪大学）
1. はじめに
粒子法は近年の計算機の発展とともに注目されるようになってきた数値計算における離散化手法の一つである。その特徴の一つとして連続体の運動を粒子の挙動によって表現するということが挙げられる。この時，連続体を離散化した各粒子は，速度や圧力，温度といった変数を保持しつつ移動する。これは従来数値計算によく利用されている有限要素法や有限差分法等の格子法にはない特徴である。粒子法は特に自由界面の大変形を伴うような流体計算に良く利用されている。例えば有限要素法で，自由界面の大変形を表現するためには，時々刻々変化する界面挙動に合わせて計算格子を都度再構築する必要があり計算格子がつぶれてしまうという危険がある。粒子法では計算点自身が物質と共に移動するため複雑に変動する界面を比較的容易に追跡することが可能である。例えば図1 に示すような二つの液滴の離散化を考えるとき，有限要素法では液滴間の斜線部に格子を配置するか否かの判断が必要であるが，粒子法ではその判断の必要は無い。またこの特徴は，離散化すべき微分方程式の表現形式にも影響する。例えば，一般的な格子法で用いられるナビエ-ストークスの方程式はオイラー法で(1)式のように表現される。
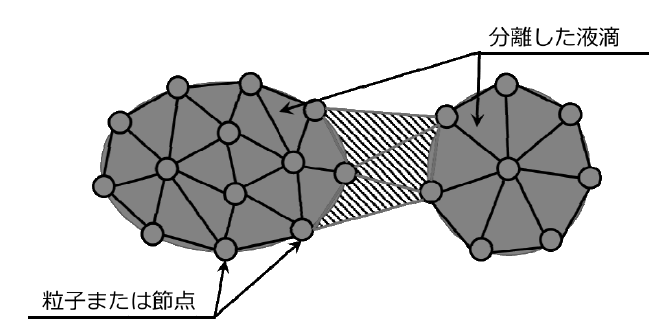
図1 有限要素法と粒子法の違い
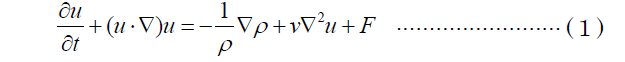
これに対して粒子法ではラグランジュ法を用いて(2)式のように表現される。
これらを見て判るように，(1)式には左辺第2 項に移流項と呼ばれる項がある。格子法では，この移流項の取り扱い方に注意が必要となり，安定な計算の妨げになるケースがある。一方粒子法では微分方程式からこの項が無くなるため，このことは離散化に対する大きなメリットの一つであると言える。