用語解説 第171回テーマ：区分線形近似
tweet
facebook
LINE
ブックマーク
コピー
印刷2025/06/06
益田 泰輔〔名城大学〕
1. 区分線形近似
近年の計算技術の発展はめざましく，さまざまな計算ソルバが開発・実用化されている。最適化計算においては，最適化問題をどのように定式化するかによって適用可能な計算ソルバが決まる。区分線形近似は，非線形な関数や制約条件の一部を線形に近似することで，より高速性や求解性が高い問題に変換するための工夫の一つである。この際，複数の区分を設定して線形近似することで，変換前の関数や制約条件により近い問題に近似することが可能である。
2. 発電機起動停止計画問題への応用
本稿では，電力系統工学分野における区分線形近似の適用事例として，発電機起動停止計画問題への応用(1)について紹介する。
一般に，発電機起動停止計画問題の目的関数は燃料費の最小化を含むが，発電機の燃料費関数は(１)式に示すような発電機出力の二次関数で表されるため，これが問題を複雑化している。
ここで，FCiは火力機iの燃料費関数（係数ai，bi，ci），pi,tは火力機iの時刻tにおける出力である。この燃料費関数を(２)～(４)式に示すように区分線形近似することで，同問題を混合整数線形計画問題として定式化することができる。
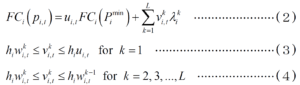
ここで，ui,tは時刻tにおける火力機iの運転状態を表すバイナリ変数（停止：0，運転：1）である。Piminは火力機iの最小出力である。Lは区間総数で，Lの数を大きくするほど近似性が高まるが計算負荷が大きくなる。λkiは火力機iの区間kにおける出力に対する燃料費の割合，vki,tは時刻tにおける火力機iの区間kにおける出力（連続変数），hi は火力機iの区間ごとの出力範囲の大きさである。wki,tはvki,tの大きさによって決まるバイナリ変数である。
このように，二次関数を区分線形近似することで，単に線形近似する場合より近似性を高く保ち，発電機起動停止計画問題における計算の高速性や求解性を向上できる。
文献
(１) 吉岡大晶・西尾晃二・高橋康平・益田泰輔・Rajitha Udawalpola・大竹秀明：「太陽光発電予測・実際値に基づく発電機と蓄電池のリアルタイム需給計画更新・需給運用」，電学論B，Vol.142, No.11, pp.505-517 (2022)