用語解説　第177回テーマ：汎化誤差

高松　尚宏 〔（国研）産業技術総合研究所〕

1. 統計的学習理論

発電量や需要の予測を目的として，過去のデータから特定のパターンを抽出して数理モデル（予測関数）を構成することがある。このようなデータに基づく予測関数の推定の理論的な枠組みを統計的学習理論と呼ぶ。

2. 経験誤差と汎化誤差

発電量や需要の予測を目的として，過去のデータから特定のパターンを抽出して数理モデル（予測関数）を構成することがある。このようなデータに基づく予測関数の推定の理論的な枠組みを統計的学習理論と呼ぶ。説明変数X と目的変数Y を入力空間X，出力空間Yから得られる確率変数とした時，データ集合は(X, Y ) ∈ X×Yと表すことができ，これは未知の同時分布P に従うと考えられる。そして，手元には観測によって， n 個のサンプル{(x₁ , y₁), (x₂ , y₂), … , (x_n , y_n)}があるとする。教師あり学習は，観測から予測関数 h : X→ Yを推定する問題と言える。
予測関数を適用した時，これを評価するための尺度として予測とサンプルから実数値を出力する関数を損失関数l :Y×Y→R(実数)として採用することとする。この時，予測関数のリスクとして以下の2 つの定式化ができる

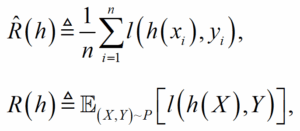
ここで，前者を経験誤差と呼び，後者を汎化誤差と呼ぶ。汎化誤差は母集団に対する期待値を表しているのに対し，経験誤差は手元のサンプルから直接得られる実現値であり，これは汎化誤差の不偏推定量に相当する。
予測関数推定の目標は，関数集合（仮説集合）H の中の候補から汎化誤差を最小化する関数h* ∈H を選択することである。しかし，汎化誤差を正確に得ることは困難である。そのため，汎化誤差の代わりに経験誤差を最小化して，最適な予測関数の推定hˆ∈H を得る。これにより推定された関数hˆと真の最適関数h*について，Rˆ (hˆ) ≤ Rˆ (h*)となるため，汎化誤差のギャップは以下のように上限が与えられる。

このうち，Rˆ (h*) – R (h*)は，

で収束することが知られている。
特に， Rˆ (hˆ ) – R (hˆ )は経験誤差最小化で推定された予測関数の期待性能（汎化誤差）のギャップに相当し，この上界について，VC 次元やRademacher 複雑度によって評価をすることが可能である。

【電気学会論文誌B，145巻，12号，2025に掲載】

用語解説のまとめページ